Grade 11 Analytical Geometry Exercise 2 Solutions | Basic Mathematics Grade XI by Sukunda Pustak Bhawan

In this page, you can find the complete solutions of the second exercise of Analytical Geometry chapter from Basic Mathematics Grade XI book published and distributed by Sukunda Pustak Bhawan.

In the above-mentioned book, analytical geometry is the 9th chapter and has two exercises only. Out of which, this is the solution of the second exercise.

Check: Basic Mathematics Grade 11 (Sukunda Publication) Guide:

Grade 11 Basic Mathematics by Sukunda Pustak Vawan Notes and Solutions | Nepal

 

Disclaimer:

Answers mentioned here are not solved by teachers. These are the solutions written by a student of Grade 11. Answers are all correct. However, the language or process of solving the questions might be informal and in examinations, you might have to add little more language and show more calculations than what has been done here. So, we highly encourage you to view these solutions as guide rather than just copying everything mentioned here. Few questions have been typed while most of them have been updated as pictures.

SOLUTIONS WILL BE ADDED SOON

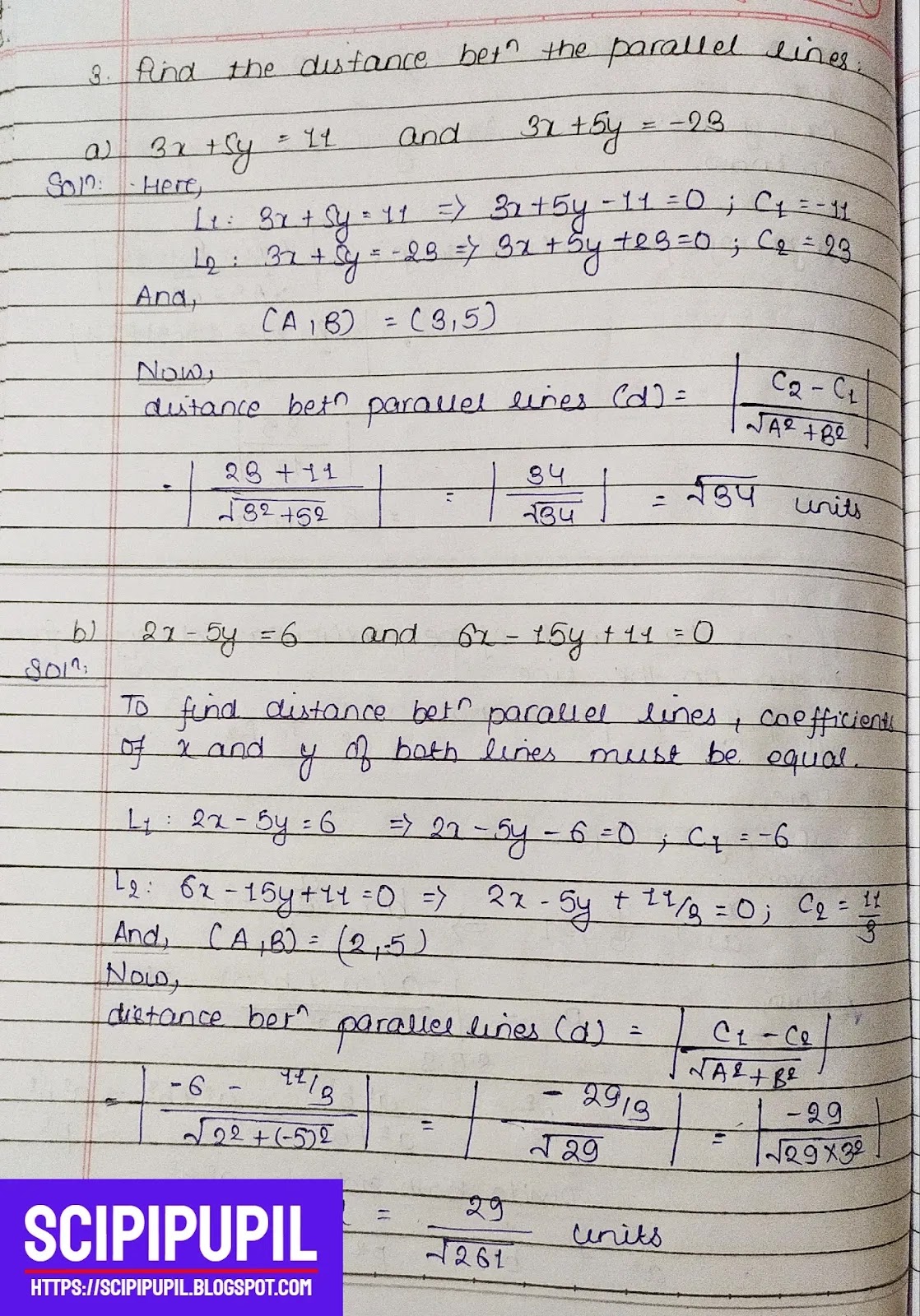
1. Find the length of perpendiculars drawn from

a) (0,0) to the line 3x + y + 1 = 0

Solution:

Here,

$(x_1,y_1) = (0,0)$

$Ax + By + C = 3x + y + 1$

Now,

Let the length of perpendicular be p

$p = \left | \dfrac{Ax+By+C}{\sqrt{A^2 + B^2}} \right |$

$or, p = \left | \dfrac{3(0) + 1(0) +1}{\sqrt{3^2 + 1^2}} \right|$

$or, p = \left | \dfrac{1}{\sqrt{10}} \right|$

$\therefore p = \dfrac{1}{\sqrt{10}} $

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

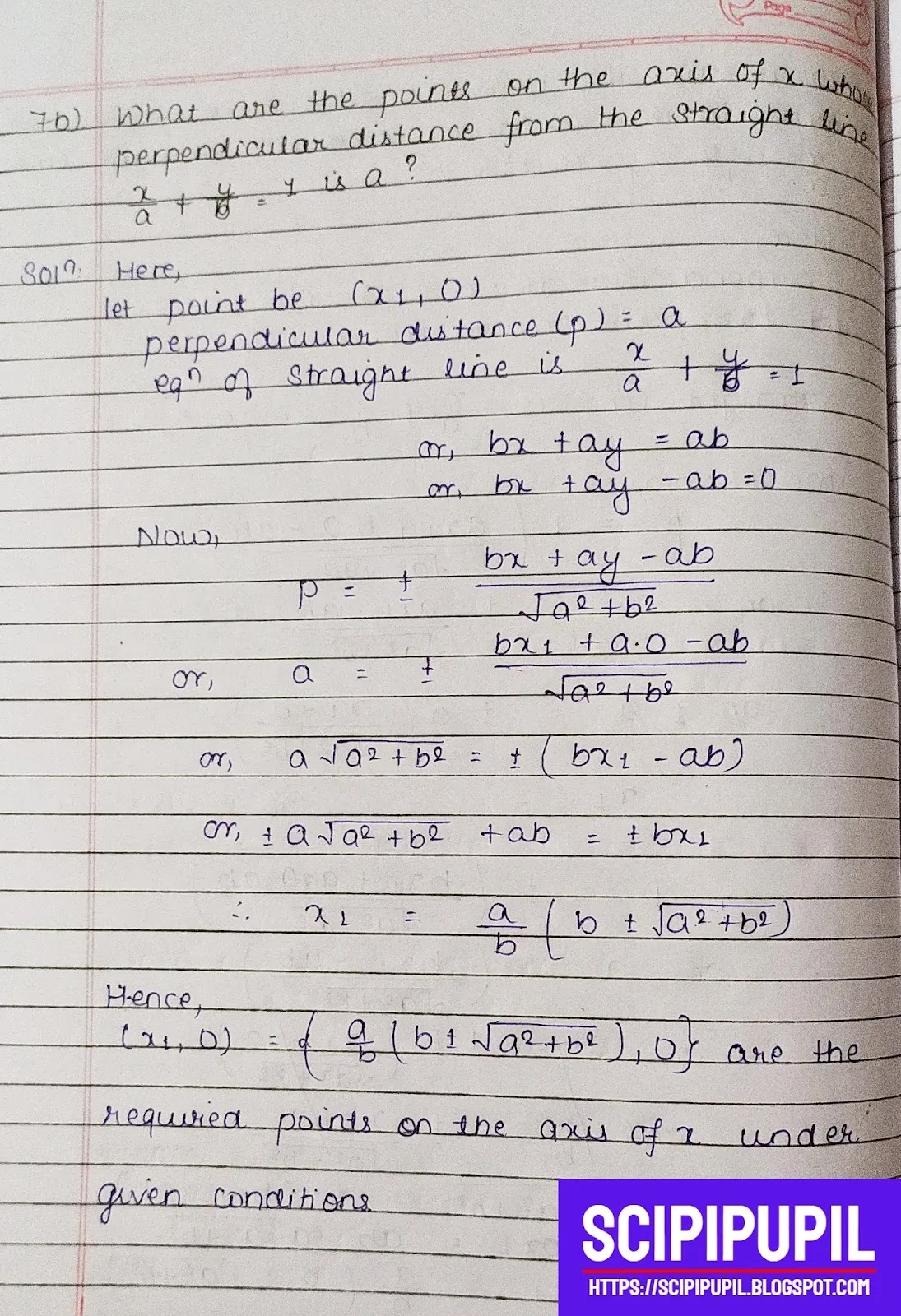
11. The origin is a corner of a square and two of its sides are $y + 2x = 0$ and $ y + 2x =3$. Find the equation of the other two sides.

Let us quickly recall:

• Opposite sides of a square are parallel to each other.

Solution:

Here,

Side 1 (OA): $y + 2x = 0$

Side 2 (BC): $y + 2x = 3$

Representation of given SQUARE

Origin is a corner of square. Putting (x,y) = (0,0) in equations of side 1 and side 2, we get to know that the side 2 does not contain origin but side 1 does contain the origin. Therefore, we draw a figure alongside representing the given square.

From figure,

$OC \perp OA$

So, equation of OC is $x - 2y = 0$

And,

$AB \perp OC$ but it does not pass through the origin. So, let the equation of AB be $x - 2y + c = 0$

In a square, perpendicular distance between OA and BC = perpendicular distance between OC and AB

$or, \dfrac{-3}{\sqrt{5}} = \dfrac{|c|}{\sqrt{5}}$

$\therefore c = \pm 3$

Hence, the required equation of line AB is $x - 2y \pm 3 = 0$ 

---

About the Textbook:

Name: Basic Mathematics Grade XI

Author(s): D.R. Bajracharya | R.M. Shresththa | M.B. Singh | Y.R. Sthapit | B.C. Bajracharya

Publisher: Sukunda Pustak Bhawan (Bhotahity, Kathmandu)

Telephone: 5320379, 5353537

Price: 695 /- (2078 BS)

Website: Sukunda Publication – Sukunda Pustak Bhawan

Buy this book: Basic Mathematics : Grade XI – Sukunda Publication