Grade 11 Sum of Infinite Geometric Series Exercise 2 Solutions | Basic Mathematics Grade XI by Sukunda Pustak Bhawan

In this page, you can find the complete solutions of the second exercise of Sequence and Series chapter from Basic Mathematics Grade XI book published and distributed by Sukunda Pustak Bhawan.

In the above-mentioned book, sequence and series is the 4th chapter and has two exercises only. Out of which, this is the solution of the second exercise in which we have to deal with the sum of infinite geometric series.

Related Solutions:

Grade 11 Basic Mathematics by Sukunda Pustak Vawan Notes and Solutions | Nepal

Grade 11 Sequence and Series Exercise 1 Solutions | Basic Mathematics Grade XI by Sukunda Pustak Bhawan

Disclaimer:

Answers mentioned here are not solved by teachers. These are the solutions written by a student of Grade 11. Answers are all correct. However, the language or process of solving the questions might be informal and in examinations, you might have to add little more language and show more calculations than what has been done here. So, we highly encourage you to view these solutions as guide rather than just copying everything mentioned here. Few questions have been typed while most of them have been updated as pictures.

Unit 4 Sequence and Series

Part 2 Sum of Infinite Geometric Series

---

1. Decide which infinite series have sums:

For an infinite series to have a sum, it must be a geometric series and its common ratio must be greater than -1 and less than 1.

a) $1 + 2 + 2^2 + 2^3 + ...$

No, this series doesn't have a finite sum because its common ratio (r) = 2 which does not satisfy the relation $|r| < 1$.

b) $1 + (-1) + 1 + (-1) + .... $

No, this series doesn't have a finite sum because its common ratio (r) = -1 which does not satisfy the relation $|r| < 1$.

c) $1 + \dfrac{1}{3} + \dfrac{1}{3^2} + \dfrac{1}{3^3} + ....$

Yes, this series has a finite sum because its common ratio (r) = $\dfrac{1}{3}$ which satisfies the relation $|r| < 1$.

d) $3 + \dfrac{3}{2} + \dfrac{3}{4} + \dfrac{3}{8} + ..$

Yes, this series has a finite sum because its common ratio (r) = $\dfrac{1}{2}$ which satisfies the relation $|r| < 1$.

e) $0.6 + 0.06 + 0.006 + ...$

Yes, this series has a finite sum because its common ratio (r) = $\dfrac{1}{10}$ which satisfies the relation $|r|<1$.

---

2. Find the sum of each of the following geometric series.

a) 16 + 8 + 4 + 2 + ..

Solution:

Here,

$a = 16$

$r = \frac{8}{16} = \frac{1}{2}$

Given series is an infinite geometric series.

Now,

$S_{\infty} = \dfrac{a}{1-r} = \dfrac{16}{1 - \frac{1}{2}}$

$= \dfrac{16}{\frac{1}{2}}$

$= 16 * 2$

$= 32$

---

---

---

---

---

---

---

---

4. Prove that

$3^{\frac{1}{3}} . 3^{\frac{1}{9}} . 3^{\frac{1}{27}} ..... = \sqrt{3}$

Solution:

To prove: $3^{\frac{1}{3}} . 3^{\frac{1}{9}} . 3^{\frac{1}{27}} ..... = \sqrt{3}$

LHS

$3^{\frac{1}{3}} . 3^{\frac{1}{9}} . 3^{\frac{1}{27}} ..... $

$= 3^{\frac{1}{3} + \frac{1}{9} + \frac{1}{27} + ....}$

The exponent of 3 forms an infinite geometric series where $a = \frac{1}{3}$ and $r = \frac{1}{3}$

So, applying the formula and continuing the solve, we get,

$= 3^{\frac{a}{1 -r}} \implies 3^{\dfrac{ \frac{1}{3} }{1 - \frac{1}{3}} }$

$ = 3^{ \frac{ \frac{1}{3} }{ \frac{2}{3}}}$

$= 3^{\frac{1}{3} * \frac{3}{2}}$

$= 3^{\frac{1}{2}}$

$= \sqrt{3}$

= RHS proved

---

5. If $x = \dfrac{1}{1+ y}, y > 0$ prove that $x + x^2 + x^3 + ... \infty = \dfrac{1}{y}$.

Solution:

Given,

$x = \dfrac{1}{1+y}, y>0$

To prove: $x + x^2 + x^3 + ... \infty = \dfrac{1}{y}$

Taking LHS

$= x + x^2 + x^3 + --- \infty$

Given  expression forms an infinite geometric series whose $a= x$ and $r = x$. using formula for sum of infinite Geometric Series, we get,

$= \dfrac{a}{1-r} \implies \dfrac{x}{1 - x}$

Put value of x from given

$= \dfrac{ \dfrac{1}{1 + y} }{1 - \dfrac{1}{1 + y}}$

$= \dfrac{1}{1 + y} * \dfrac{1}{1 - \dfrac{1}{1 + y}}$

$= \dfrac{1}{1 + y} * \dfrac{1}{ \dfrac{1 + y -1}{1 + y}}$

$= \dfrac{1}{1 + y} * \dfrac{ 1+y}{1+ y-1}$

$= \dfrac{1}{1 + y} * \dfrac{1+ y}{y}$

$= \dfrac{1}{y}$

RHS

---

---

---

---

---

---

---

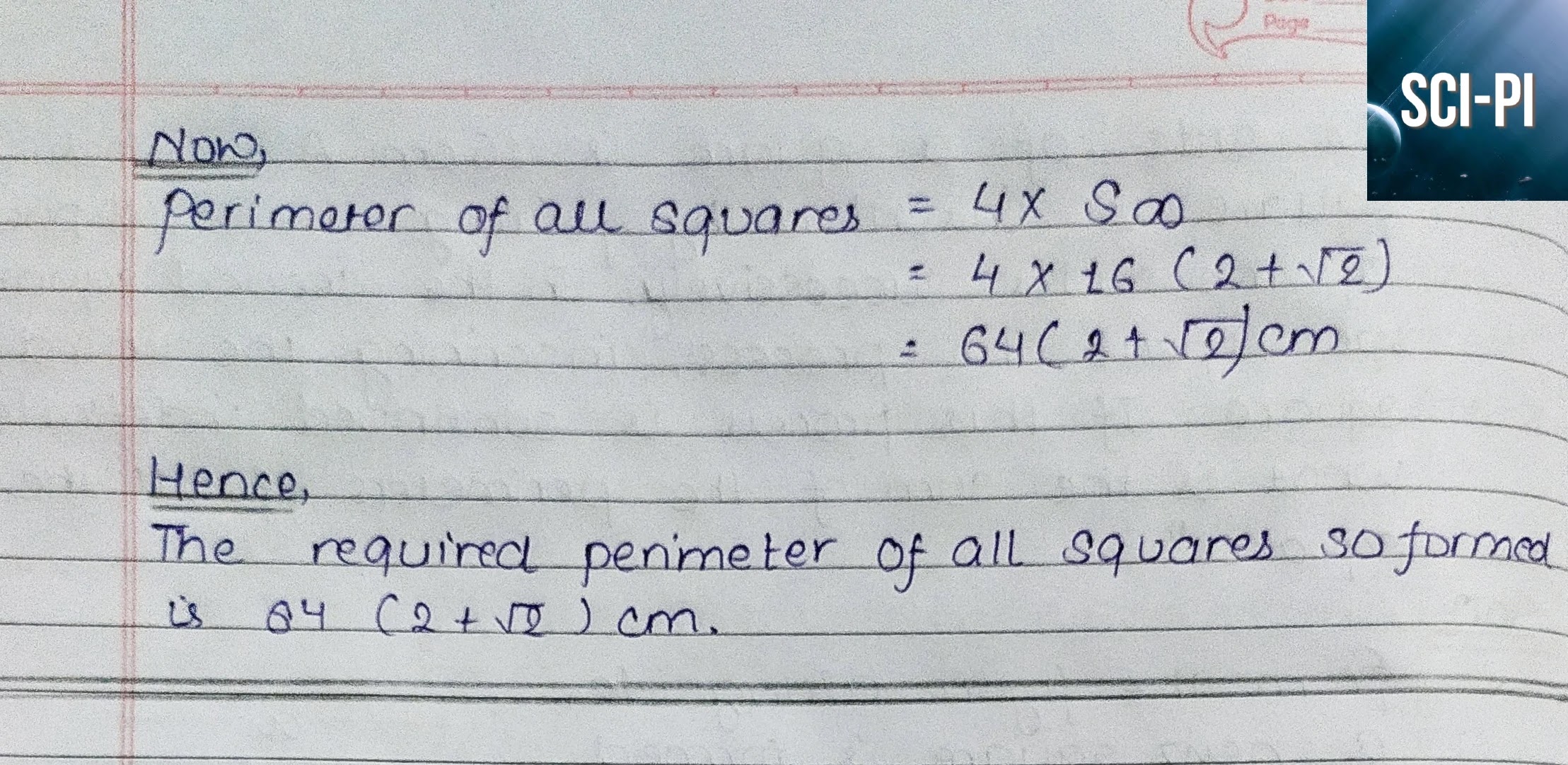
About the Textbook:

Name: Basic Mathematics Grade XI

Author(s): D.R. Bajracharya | R.M. Shresththa | M.B. Singh | Y.R. Sthapit | B.C. Bajracharya

Publisher: Sukunda Pustak Bhawan (Bhotahity, Kathmandu)

Telephone: 5320379, 5353537

Price: 695 /- (2078 BS)

Website: Sukunda Publication – Sukunda Pustak Bhawan

Buy this book: Basic Mathematics : Grade XI – Sukunda Publication