Exercise 7.3 Surface Area and Volume of Cones Class 10 Solutions

Exercise 7.3 Surface Area and Volume of Cones

The above-mentioned topic is mentioned in the vedanta Excel in Mathematics book in Unit 7 - the third part of Mensuration where we deal with the surface area and volumes of Triangular Prisms, Pyramids and Cones, along with basic Household Mensuration exercises.

Here is a complete solution of exercise 7.3 from vedanta's book for Class 10 students. All solutions are accurate but there might be bad handwriting or extra crossing in many solutions. In case you do not understand the handwriting, numerical or language, do let us know in the comment section so that we can make it clear to you.

We have almost all solutions from vedanta Excel in Mathematics Book 10 for Grade 10 students. We also have notes and other unit tests in it. If you want to see it, visit here:

vedanta Excel in Mathematics Class 10 Guide Book, Notes, and Solutions (scipipupil.blogspot.com)

Get solutions of other exercises from this unit by visiting the links mentioned just below:

Now, let us get into the solutions of Exercise 7.3 Surface Area and Volume of Cones Class 10.

General Section

1 a)

Solution:

Here,

radius (r) = a

slant height (l) = b

Curved surface area of cone (CSA) = $\pi rl$ = $\pi ab$

1 b)

Solution:

Here,

radius (r) = x

slant (height) = y

Total surface area of cone (TSA) = $\pi r(r+l)$ = $\pi x(x+y)$

2 a)

Solution:

Here,

slant height (l) = 15 cm

radius (r) = 7 cm

Curved surface area of cone (CSA) = $\pi rl$ = $\dfrac{22}{7}*7*15$ = $330 cm^2$

2 b)

Solution:

Here,

radius (r) = 14 cm

slant height (l) = 20 cm

Total surface area of cone (TSA) = $\pi r(r+l)$ = $\dfrac{22}{7} * 14 * (14 + 20)$ = $1496 cm^2$

2 c)

Solution:

Here,

vertical height (h) = 21 cm

diameter (d) = 14 cm

radius (r) = d/2 = 7 cm

Volume of cone (V) = $\dfrac{1}{3} \pi r^2h$ = $\dfrac{1}{3} * \dfrac{22}{7} * 7^2 * 21$ = $1078 cm^3$

3 a)

Solution:

Here,

slant height (l) = 5 cm

radius (r) = 3 cm

vertical height (h) = $\sqrt{l^2 - r^2}$

$= \sqrt{5^2 - 3^2}$

$= 4 cm$

Now,

Volume of cone (V) = $\dfrac{1}{3} \pi r^2h$ = $\dfrac{1}{3} * \dfrac{22}{7} * 3^2 *4$ = $37.71 cm^3$

3 b)

Solution:

Here,

vertical height (h) = 7 cm

radius (r) = 24 cm

slant height (l) = $\sqrt{h^2 + r^2}$ = $\sqrt{7^2 + 24^2}$ = $25 cm$

Now,

Curved surface area of the cone (CSA) = $\pi rl$ = $\dfrac{22}{7} * 7 * 25$ = $550 cm^2$

3 c)

Solution:

Here,

vertical height (h) = 48 cm

slant height (l) = 50 cm

radius (r) = $\sqrt{l^2 - h^2}$ = $\sqrt{50^2 - 48^2}$ = $14cm$

Now,

Total surface area of the cone (TSA) = $\pi r(r+l)$ = $\dfrac{22}{7} * 14 * (14 + 50)$ = $2816 cm^2$

Page 1 of 17

Exercise 7.3 Surface Area and Volume of Cone Class 10 Solutions | vedanta Excel in Mathematics

Page 2 of 17

Page 3 of 17

Page 4 of 17

Page 5 of 17

Page 6 of 17

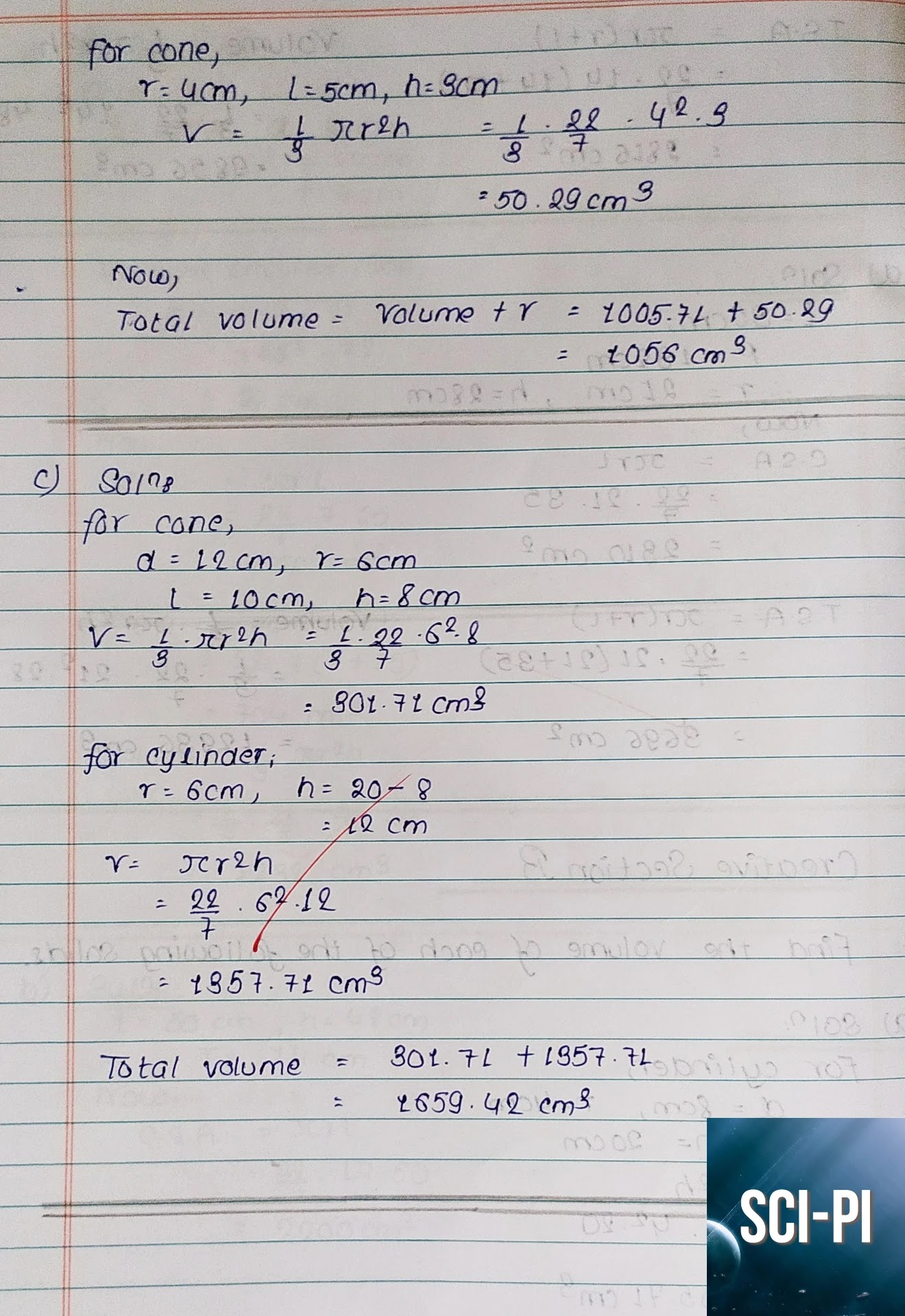
Page 7 of 17

Page 8 of 17

Page 9 of 17

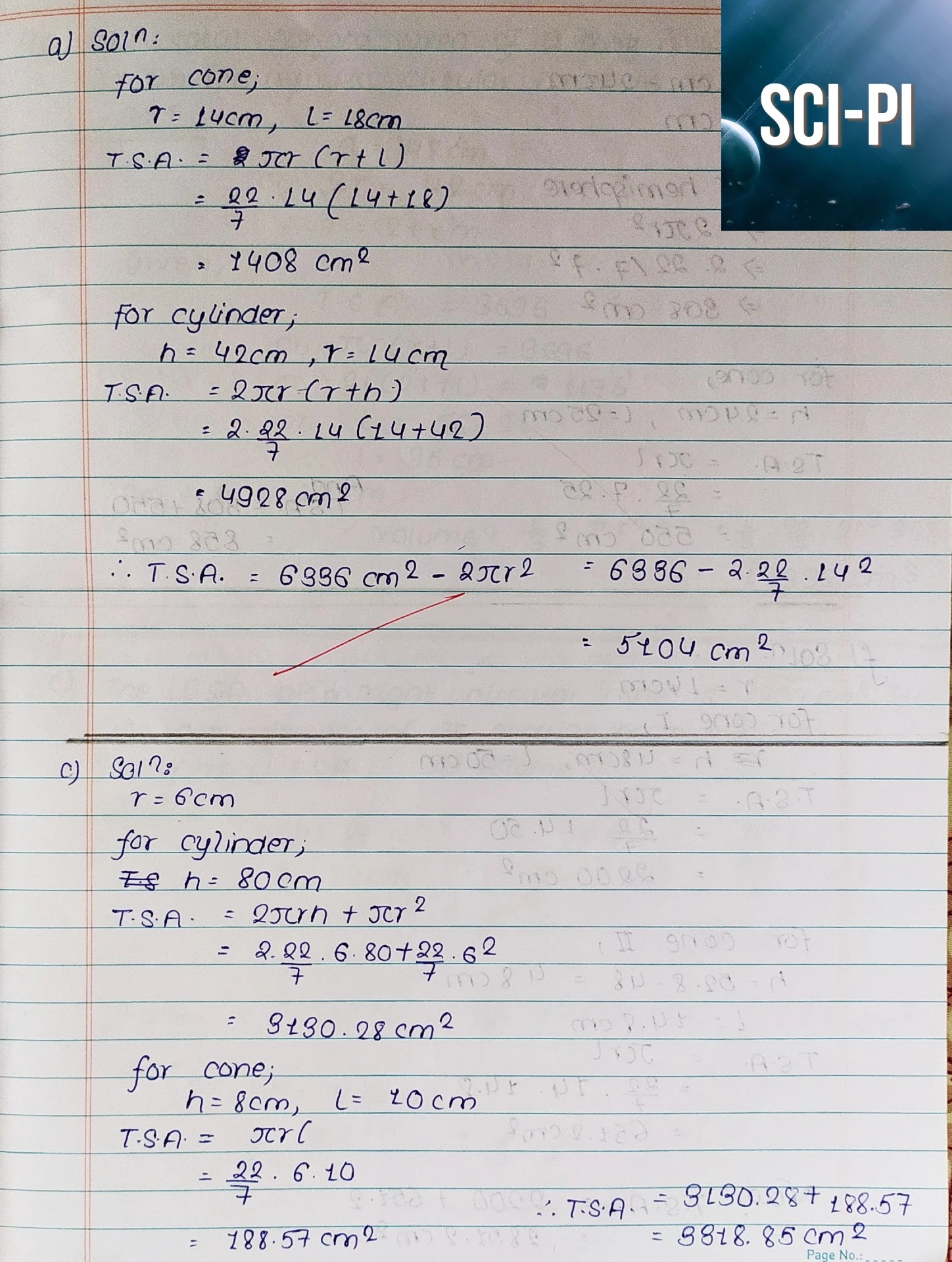
Page 10 of 17

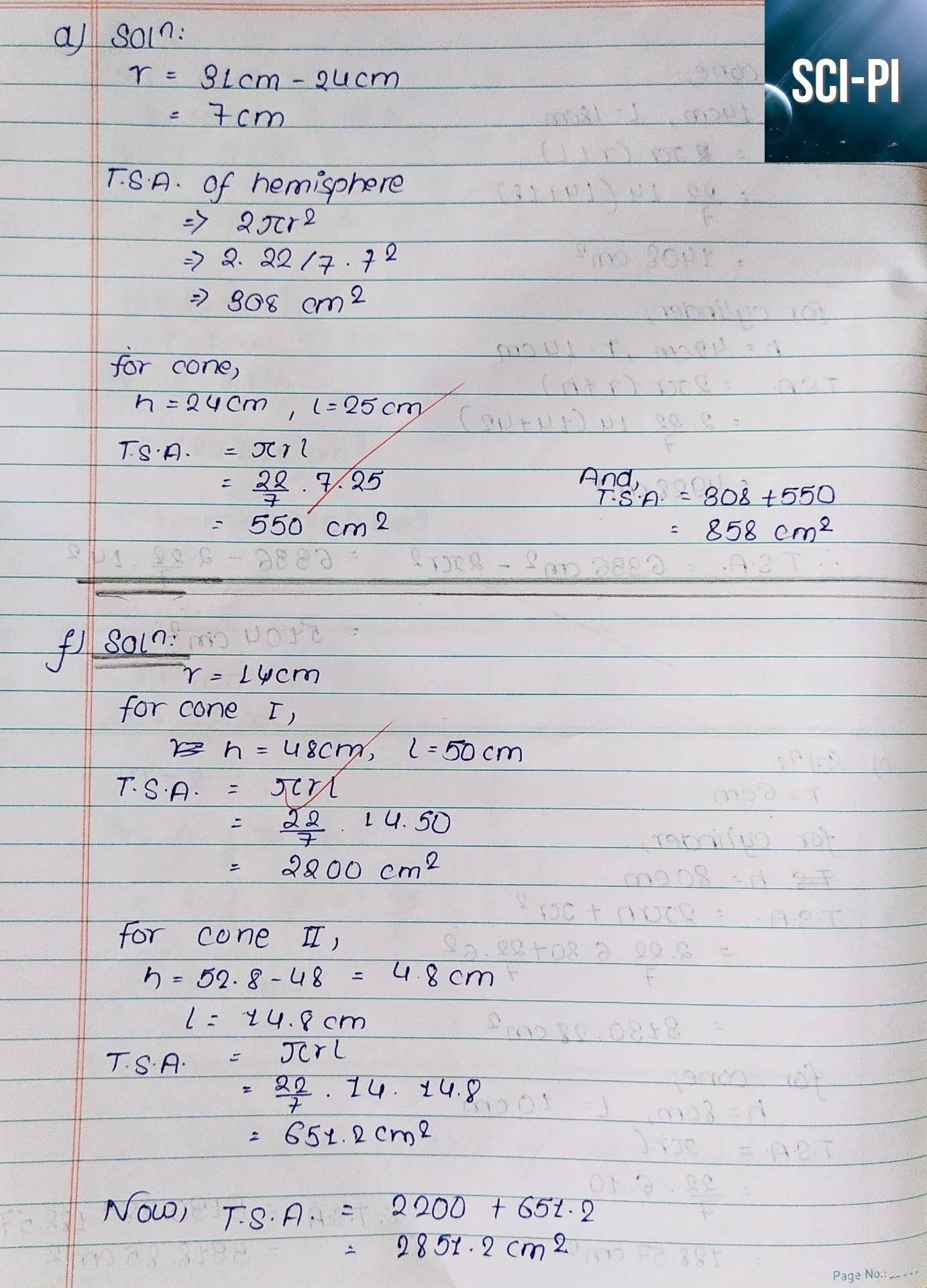
Page 11 of 17

Page 12 of 17

Page 13 of 17

Page 14 of 17

Page 15 of 17

Page 16 of 17

Page 17 of 17

About vedanta EXCEL in MATHEMATICS Book 10

Author: Hukum Pd. Dahal

Editor: Tara Bahadur Magar

Vedanta Publication (P) Ltd.

Vanasthali, Kathmandu, Nepal

+977-10-4382404, 01-4362082

vedantapublication@gmail.com

About this page:

Exercise 7.3 Surface Area and Volume of Cones Class 10 Solutions | vedanta Excel in Mathematics is a collection of the solutions related to calculation of surface area and volume of cones which is a 3 dimensional figure from Mensuration (III): Prisms and Pyramids chapter for Nepal's Secondary Education Examination (SEE) appearing students.

#Class10

Exercise 7.3 Surface Area and Volume of Cones Class 10 Solutions | vedanta Excel in Mathematics

Exercise 7.3 Surface Area and Volume of Cones