In this page, you can find the complete solutions of the second
exercise of Circle chapter from Basic Mathematics Grade XI book
published and distributed by Sukunda Pustak Bhawan.
In the above-mentioned book, circle is the 11th chapter and has two
exercises only. Out of which, this is the solution of the second
exercise.
Check: Grade 11 Circle Exercise 1 Complete Solutions
Check: Basic Mathematics Grade 11 (Sukunda Publication)
Guide:
Grade 11 Basic Mathematics by Sukunda Pustak Vawan Notes and Solutions | Nepal
Disclaimer:
Answers mentioned here are not solved by teachers. These are the
solutions written by a student of Grade 11. Answers are all correct.
However, the language or process of solving the questions might be
informal and in examinations, you might have to add little more language
and show more calculations than what has been done here. So, we highly
encourage you to view these solutions as guide rather than just copying
everything mentioned here.
1. Find the equations of tangents and normal to the following
circles.
a) $x^2 + y^2 = 8$ at $(2,2)$
Solution:
Here,
$(x_1,y_1) = (2,2)$
Equation of circle $\implies x^2 + y^2 = 8$
Comparing equation of circle with standard equation of circle $x^2 + y^2 =
a^2$, we get, $a^2 = 8$
Now,
Equation of tangent $\implies xx_1 + yy_1 = a^2$
$\implies x(2) + y(2) = 8$
$\implies x + y = 4$
And,
Equation of normal $\implies xy_1 = yx_1$
$\implies x(2) = y(2)$
$\implies x = y$
$\implies x- y = 0$
b) $x^2 + y^2 = 36$ at $(-6,0)$
Solution:
Here,
$(x_1,y_1) = (-6,0)$
Equation of circle $\implies x^2 + y^2 = 36$
Comparing equation of circle with standard equation of circle $x^2 + y^2
= a^2$, we get, $a^2 = 36$
Now,
Equation of tangent $\implies xx_1 + yy_1 = a^2$
$\implies x(-6) + y(0) = 36$
$\implies -6 x= 36$
$\implies x = -6$
And,
Equation of normal $\implies xy_1 = yx_1$
$\implies x(0) = y(-6)$
$\implies 0 = -6y$
$\implies y = 0$
c) $x^2 + y^2 - 6x -8y -4 = 0$ at $(8,6)$
Solution:
Here,
$(x_1,y_1) = (8,6)$
Equation of circle $\implies x^2 + y^2 -6x - 8y - 4=0$
Comparing equation of circle with standard equation of circle $x^2 + y^2
+ 2gx + 2fy + c =0$, we get, $g= -3, f= -4, c = -4$
Now,
Equation of tangent $\implies xx_1 + yy_1 + g(x+ x_1) + f(y+y_1) + c =
0$
$\implies x(8) + y(6) + (-3)(x + 8) + (-4)(y + 6) + (-4) = 0$
$\implies 8x + 6y -3x -24 -4y -24 -4 = 0$
$\implies 5x + 2y -52 = 0$
And,
Equation of normal $\implies (y- y_1) = \dfrac{y_1 + f}{x_1 + g} (x
-x_1)$
$\implies (y-6) = \dfrac{6+ (-4)}{8+ (-3)} (x-8)$
$\implies (y-6) = \dfrac{2}{5} (x-8)$
$\implies 5(y-6) = 2(x-8)$
$\implies 5y -30 = 2x - 16$
$\implies 2x - 5y +14 =0$
2 a) Find the equation of the tangent to the circle $2x^2 + 2y^2 = 9$ which makes angle 45 with the x-axis.
Solution: Here, $\theta = 45^o$
So, $m = tan \theta = tan 45^o = 1$
And,
Equation of circle: $2x^2 + 2y^2 = 9$
$\implies x^2 + y^2 = \dfrac{9}{2}$
So, a = \sqrt{\dfrac{9}{2}}$
Now,
Equation of tangent to the given circle is:
$y = mx \pm a \sqrt{1 + m^2}$
$or, y = 1x \pm \dfrac{3}{\sqrt{2}} \sqrt{1 + 1^2}$
$or, y = x \pm \dfrac{3}{\sqrt{2}} * \sqrt{2}$
$\therefore y = x \pm 3$ is the required equation of the tangent.
3 a) Show that the lines $3x - 4y = 25$ and the circle $x^2 + y^2 = 25$ interesect in two coincident points.
Solution:
Given, line: $3x - 4y = 25$
$\implies y = \dfrac{3x - 25}{4}$
And, circle: $x^2 + y^2 = 25$
Put value of y in equation of circle,
$x^2 + \left ( \dfrac{3x - 25}{4} \right)^2 = 25$
$or, x^2 + \dfrac{9x^2 - 2*3x*25 + 25^2}{16} = 25$
$or, 16x^2 + 9x^2 - 150x + 625 = 400$
$or, 25x^2 - 150x + 225 = 0$
$or, 25x^2 - 2*5*15*x + 15^2 = 0$
$or, (5x - 15)^2 = 0$
$or, 5x = 15$
$\therefore x = 3$
Again,
$y = \dfrac{3*3 -25}{4}$
$or, y = \dfrac{9-25}{4}$
$or, y = \dfrac{-16}{4}$
$\therefore, y = -4$
Since, the equation of circle is quadratic, the solution must have two points. However, we obtained only one set of points, i.e. (x,y) = (3,-4), thus, we can say that the line touches the circle in two coincident points.
Coincident points refer to the overlapping of the points on the same cartesian point.
4. Find the equation of the tangents to the circle.
a) $x^2 + y^2 = 4$, which are parallel to $3x+4y-5 = 0$
Solution:
Given, tangents are parallel to $3x + 4y - 5=0$
$\implies$ slope of tangents = slope of the parallel line
$\implies$ slope of tangents $(m) = \dfrac{-3}{4}$
And,
Equation of circle: $x^2 + y^2 = 4$
Here, $a^2 = 4$ $\implies a = 2$
Now,
Equation of tangents is as follows:
$y = mx \pm a \sqrt{1 + m^2}$
$or, y = \dfrac{-3}{4}x \pm 2 \sqrt{ 1 + \left ( \dfrac{-3}{4} \right)^2 }$
$or, y = \dfrac{-3}{4}x \pm 2 \sqrt{ 1 + \dfrac{9}{16} }$
$or, y = \dfrac{-3}{4}x \pm 2 \sqrt{ \dfrac{25}{16}}$
$or, y = \dfrac{-3}{4}x \pm 2 * \dfrac{5}{4}$
$or, y = \dfrac{-3x \pm 10}{4}$
$or, 4y = -3x \pm 10$
$\therefore 3x + 4y \pm 10 = 0$ is the required equation of tangent.
5 a) Find the value of k so that the line $4x + 3y + k = 0$ may touch the circle $x^2 + y^2 - 4x + 10y + 4 = 0$
Solution:
The line touches the circle if the perpendicular distance from the centre of the circle on the line is equal to the radius of the circle.
Here,
Equation of circle: $x^2 + y^2 -4x + 10y + 4 =0$
So, centre of circle $(-g,-f) = (2, -5)$
Radius of circle $r = \sqrt{g^2 + f^2 -c}$
$or, r = \sqrt{ (-2)^2 + 5^2 - 4}$
$or, r = \sqrt{4 + 5^2 -4}$
$\therefore r = 5$
And,
Line: $4x + 3y + k = 0$
$\implies A = 4 \text{and} B = 3$
Now,
$\dfrac{|A(-g) + B(-f) + k|}{\sqrt{A^2 + B^2}} = r$
$or, \dfrac{|4(2) + 3(-5) + k|}{\sqrt{4^2 + (-3)^2}} = 5$
$or, \dfrac{ \pm ( 8 - 15 + k)}{5} = 5$
$or, \pm (-7 + k) = 25$
Taking positive sign,
$or, -7 + k = 25$
$\therefore k = 32 $
Taking negative sign,
$or, 7 - k = 25$
$\therefore k = -18$
Hence, the required values of k are 32 and -18.
6 b) Deduce the condition that $lx + my + n = 0$ may be a tangent to the circle $x^2 + y^2 + 2gx + 2fy + c=0$.
Solution:
A line is tangent to a circle is the perpendicular distance from the centre of the circle on the given line is equal to the radius of the circle.
Here, circle: $x^2 + y^2 + 2gx +2fy + c= 0$
Centre = $(-g,-f)$
Radius of circle $r = \sqrt{g^2 + f^2 -c}$
Given line: $lx + my + n = 0$
Now,
$\dfrac{ \pm ( l(-g) + m(-f) + n}{\sqrt{l^2 + m^2}} = r$
Squaring both sides
$or, \left ( \dfrac{ \pm -lg -mf + n}{sqrt{l^2 + m^2}} \right ) = \left ( \sqrt{g^2 + f^2 -c} \right)^2$
$or, \dfrac{(n - lg - mf)^2}{l^2 + m^2} = g^2 + f^2 -c$
$\therefore (n - lg - mf)^2 = (g^2 + f^2 -c)(l^2 + m^2)$ is the required condition for the line to the a tangent to the cricle.
7 a) Show that the tangents to the circle $x^2 + y^2 = 100$ at the points (6,8) and (8,-6) are perpendicular to each other.
Solution: We know,
Equation of tangent: $xx_1 + yy_1 = a^2$
Given, equation of circle: $x^2 + y^2 = 100$
$\implies a^2 = 100$
And,
Equation of tangent to the circle at point (6,8) is:
$6x + 8y = 100$
Slope of this tangent $(m_1) = \dfrac{-3}{4}$
Equation of tangent to the circle at point (8,-6) is:
$8x - 6y = 100$
Slope of this tangent $(m_2) = \dfrac{4}{3}$
Since, $m_1 * m_2 = -1$, given tangents are perpendicular to each other.
9. If the line $lx + my = 1$ touches the circle $x^2 + y^2 = a^2$, prove that the point (l,m) lies on a circle whose radius is $\dfrac{1}{a}$.
Solution:
Here,
Equation of line: $lx + my = 1$
$\implies lx + my - 1 = 0$ --- (i)
Equation of circle: $x^2 + y^2 = a^2$ --- (ii)
Radius of circle: $a$
Centre of circle: $(0,0)$
To prove: (l,m) satisifies the equation of circle with radius $\dfrac{1}{a}$
We know,
Length of perpendicular drawn from centre of circle (ii) on line (i) = radius of circle (ii)
$or, \pm \left ( \dfrac{l(0) + m(0) -1 }{ \sqrt{l^2 + m^2} } \right) = a$
Squaring both sides
$or, \dfrac{1}{l^2 + m^2} = a^2$
$or, l^2 + m^2 = \dfrac{1}{a^2}$ --- (iii)
From equation (iii), it can be stated dthat the point (l,m) lies on a standard cirle whose radius is $\dfrac{1}{a}$.
10 a) Find the conditions for the two circle $x^2 + y^2 = a^2$ and
$(x-c)^2 + y^2 = b^2$ to touch (i) externally and (ii) internally.
Solution:
Here,
Circle I,
Equation: $x^2 + y^2 = a^2$
Centre (c1): $(0,0)$
Radius (r1): $a$
Circle II,
Equation: $(x-c)^2 + y^2 = b^2$
Centre (c2): $(c,0)$
Radius (r2): $b$
When circles touch externally,
$c1c2 = r1 - r2$
$or, \sqrt{ (c-0)^2 + (0-0)^2} = a + b$
$or, \sqrt{c^2} = a + b$
$\therefore a + b = c$ is the required condition for the given circles I
and II to touch externally.
When circles touch internally,
$c1c2 = r1 - r2$
$or, \sqrt{ (c-0)^2 + (0-0)^2} = a - b$
$or, \sqrt{ c^2} = a - b$
c is the distance so it can never be negative.
$\therefore a \sim b = c$ is the required condition for the given circles
I and II to touch internally.
10 b) Prove that the two circles $x^2 + y^2 + 2ax + c^2 = 0$ and $x^2 +
y^2 + 2by + c^2 =0$ touch if $\dfrac{1}{a^2} + \dfrac{1}{b^2}=
\dfrac{1}{c^2}$.
Solution:
Here,
Circle I:
Equation: $x^2 + y^2 + 2ax + c^2 = 0$
Centre (c1): $(-a, 0)$
Radius (r1): $\sqrt{a^2 - c^2}$
Circle II:
Equation: $x^2 + y^2 + 2by + c^2 = 0$
Centre (c2): $(0,-b)$
Radius (r2): $\sqrt{b^2 - c^2}$
Since, it is not specified either the circles touch internally or
externally, we consider both the conditions in the same equation as:
$c1c2 = r1 \pm r2$
$or, \sqrt{ ( 0 + a)^2 + (-b - 0)^2} = \sqrt{a^2 - c^2} \pm \sqrt{b^2 -
c^2}$
Squaring both sides,
$or, ( \sqrt{ a^2 + b^2} ) ^2 = ( \sqrt{a^2 - c^2 } \pm \sqrt{b^2 - c^2}
)^2$
$or, a^2 + b^2 = (a^2 -c^2) + (b^2 - c^2) \pm 2 \sqrt{(a^2 - c^2)(b^2 -
c^2)}$
$or, 2c^2 = \pm 2 \sqrt{(a^2 - c^2)(b^2 - c^2)}$
Squaring both sides
$or, 4c^4 = 4 (a^2 -c^2)(b^2 - c^2)$
$or, c^4 = a^2b^2 - a^2c^2 - b^2c^2 + c^4$
$or, a^2b^2 = a^2c^2 + b^2c^2$
Dividing the whole equation by $a^2b^2c^2$
$or, \dfrac{a^2b^2}{a^2b^2c^2} = \dfrac{a^2c^2}{a^2b^2c^2} +
\dfrac{b^2c^2}{a^2b^2c^2}$
$or, \dfrac{1}{c^2} = \dfrac{1}{b^2} + \dfrac{1}{a^2}$
$\therefore \dfrac{1}{a^2} + \dfrac{1}{b^2} = \dfrac{1}{c^2}$
Hence, it is proved.
11. Find the equations of the tangents drawn from the point (11,3) to
the circle $x^2 + y^2 = 65$. Also, find the angle between the two
tangents.
Solution:
We know, from an exterior point to a circle, two tangents are
possible.
Here, the external point is (11,3)
So, the equation of tangents is $\implies (y - 3) = m (x - 11)$
$\implies y - 3 = mx - 11m$
$\implies mx - y - (11m -3) = 0$ --- (i)
Equation of circle is $\implies x^2 + y^2 = 65$ --- (ii)
Centre and radius of circle (ii) are $(0,0)$ and $\sqrt{65}$,
respectively.
We know,
Length of perpnedicular distance from the circle (ii) on tangent (i) =
radius of circle (ii)
$ \pm \left ( \dfrac{ m(0) - 1(0) - (11m -3)}{ \sqrt{m^2 + (-1)^2}}
\right ) = \sqrt{65}$
Squaring both sides
$or, \left ( \dfrac{3 - 11m }{ \sqrt{1 + m^2}} \right)^2 =
(\sqrt{65})^2$
$or, 9 - 66m + 121m^2 = 65(1 + m^2)$
$or, 9 - 66m + 121m^2 = 65 + 65 m^2$
$or, 56m^2 - 66m - 56 = 0$
On solving, we get, $m = - \dfrac{4}{7} \ \text{or} \ m =
\dfrac{7}{4}$
Put value of m in equation (i), we get the required equation of tangents
as follows:
When m = $\dfrac{-4}{7}$, equation of tangent $\implies \dfrac{-4}{7}x -
y - \left \{ 11 \left(\dfrac{-4}{7} \right) -3 \right \} $
$\implies 4x + 7y - 65 = 0$
When m = $\dfrac{7}{4}$, equation of tangent $\implies \dfrac{7}{4}x - y
- \left \{ 11 \left ( \dfrac{7}{4} \right) -3 \right \}$
$\implies 7x - 4y - 65 = 0$
Hence, the require equations of tangents are $(4x + 7y - 65 = 0) ---
(iii)$ and $(7x - 4y - 65 = 0) --- (iv)$
Since, the product of slopes of tangents in equation (iii) and (iv) is
-1, the angle between the tangents is 90 degrees.
12. Prove that the straight line $y = x + a \sqrt{2}$ touches the
circle $x^2 + y^2 = a^2$ and find its point of contact.
Solution:
Given,
equation of straight line $y = x + a \sqrt{2} \implies x - y + a \sqrt{2}
= 0$ --- (i)
equation of circle $x^2 + y^2 = a^2$ --- (ii)
Here,
centre of circle of equation (ii) is (0,0) and its radius is a
units.
If the line touches the circle, then the perpendicular distance from the
centre of the circle (ii) to the line (i) must be equal to the radius of
the circle (ii).
$\pm \left ( \dfrac{ 1(0) - 1(0) + a \sqrt{2}}{\sqrt{1^2 + 1^2}} \right )
= a$
Squaring both sides,
$or, \left ( \dfrac{a \sqrt{2}}{\sqrt{2}} \right ) ^2 = a^2$
$or, \dfrac{2a^2}{2} = a^2$
$\therefore a^2 = a^2$ which is true.
Hence, it is proved that the line touches the circle.
For point of contact, solving equation (i) and (ii), we get,
$x^2 + (x + a \sqrt{2})^2 = a^2$
$or, x^2 + x^2 + 2\sqrt{2}ax + 2a^2 = a^2$
$or, 2x^2 + 2 \sqrt{2}ax + a^2 = 0$
$or, (\sqrt{2}x)^2 + 2 \sqrt{2}x a + (a)^2 = 0$
$or, (\sqrt{2}x + a )^2 = 0$
$or, \sqrt{2}x = -a$
$\therefore x = - \dfrac{a}{\sqrt{2}}$
And,
Put value of x in equation (i), we get, $ y = \sqrt{a}{\sqrt{2}}$
Hence, the required point of contact is (x,y) = $\left ( -
\dfrac{a}{\sqrt{2}}, \dfrac{a}{\sqrt{2}} \right)$.
13. Tangents are drawn from the origin to the circle $x^2 + y^2 + 10x +
10y + 40 =0$. Find their equations.
Solution:
Here,
Equation of circle $\implies x^2 + y^2 + 10x + 10y + 40 =0$
Comparing above equation with general equation of circle, we get,
$Centre (-g,-f) = (-5,-5)$
$radius (r) = \sqrt{g^2 + f^2 - c} = \sqrt{5^2 + 5^2 - 40}$
$\implies r = \sqrt{10}$
We know,
Tangent is a straight line.
And,
equation of straight line passing through origin is $y = mx \implies mx -
y = 0$
So, let the equation of tangent be represented by $mx- y = 0$
Also,
Length of perpendicular = Radius of circle
$or, \pm \left ( \dfrac{mx_1 - y_1}{\sqrt{1 + m^2}} \right ) =
\sqrt{10}$
$or, \pm \left ( \dfrac{m(-g) - (-f)}{\sqrt{1 + m^2}} \right ) =
\sqrt{10}$
Squaring both sides, we get,
$or, \left ( \dfrac{m(-5) - (-5)}{\sqrt{1 + m^2}} \right )^2 =
(\sqrt{10})^2$
$or, \left ( \dfrac{-5m + 5}{\sqrt{1 + m^2}} \right )^2 = 10$
$or, 25 ( 1 - 2m + m^2) = 10(1 + m^2)$
$or, 25 - 50 m + 25m^2 = 10 + 10m^2$
$or, 25 - 50m - 10 + 25m^2 - 10m^2 = 0$
$or, 15m^2 - 50m - 15 = 0$
$or, (15m -5)(m-3) = 0$
Either, $15m - 5 = 0 \implies m = \dfrac{1}{3}$
Or, $m-3 = 0 \implies m = 3$
When $m = \dfrac{1}{3}$
Equation of tangent $\implies \dfrac{1}{3}x - y \implies x - 3y =
0$
Also $m = 3$
Equation of tangent $\implies 3x - y = 0$
Hence, the required equation of tangents are $x - 3y = 0$ and $3x- y
=0$.
14. Determine the legnth of the tangent to the circle
a) $x^2 + y^2 = 25$ from (3,5)
Solution:
Here, equation of circle $\implies x^2 + y^2 = 25$
So, the value of $a^2 = 25$
Given, $(x_1, y_1) = (3,5)$
Hence,
Length of tangent is given by
$\sqrt{x_1^2 + y_1^2 - a^2}$
$= \sqrt{3^2 + 5^2 - 25}$
$= \sqrt{9}$
$= 3$
b) $x^2 + y^2 + 4x + 6y - 19 = 0$ from (6,4)
Solution:
Here, equation of circle $\implies x^2 + y^2 +4x + 6y - 19 = 0$
Given, $(x_1, y_1) = (6,4)$
Hence,
Length of tangent is given by
$\sqrt{x_1^2 + y_1^2 + 2gx_1 + 2fy_1 + c}$
$= \sqrt{6^2 + 4^2 + 4(6) + 6(4) -19}$
$= \sqrt{36 + 16 + 24 + 24 - 19}$
$= \sqrt{81}$
$= 9$
15. Determine the value of k so that the length of the tangent from
(5,4) to the circle $x^2 + y^2 + 2ky = 0 is 5$.
Solution:
Here,
$(x_1,y_1) = (5,4)$
Equation of circle $\implies x^2 + y^2 + 2ky = 0$
Comparing above equation of circle with general equation of circle $x^2 +
y^2 + 2gx +2fy +c =0$, we get,
$2f = 2k, 2g = 0, c = 0$
We know,
Length of tangent is
$5 = \sqrt{x_1^2 + y_1^2 +2gx_1 + 2fy_1 + c}$
$5 = {5^2 + 4^2 + 0(5) + 2k(4) + 0}$
$5^2 =({25 + 16 + 8k})^2$
$or, 25 = 25 + 16 + 8k$
$or, -16 = 8k$
$\therefore k = -2$
Hence, the required value of k is -2.
16. Show that the length of the tangent drawn from any point on the
circle $x^2 + y^2 + 2gx + 2fy + c= 0$ to the circle $x^2 + y^2 + 2gx +
2fy + c_1 = 0$ is $\sqrt{c_1 -c}$.
Solution:
According to the question,
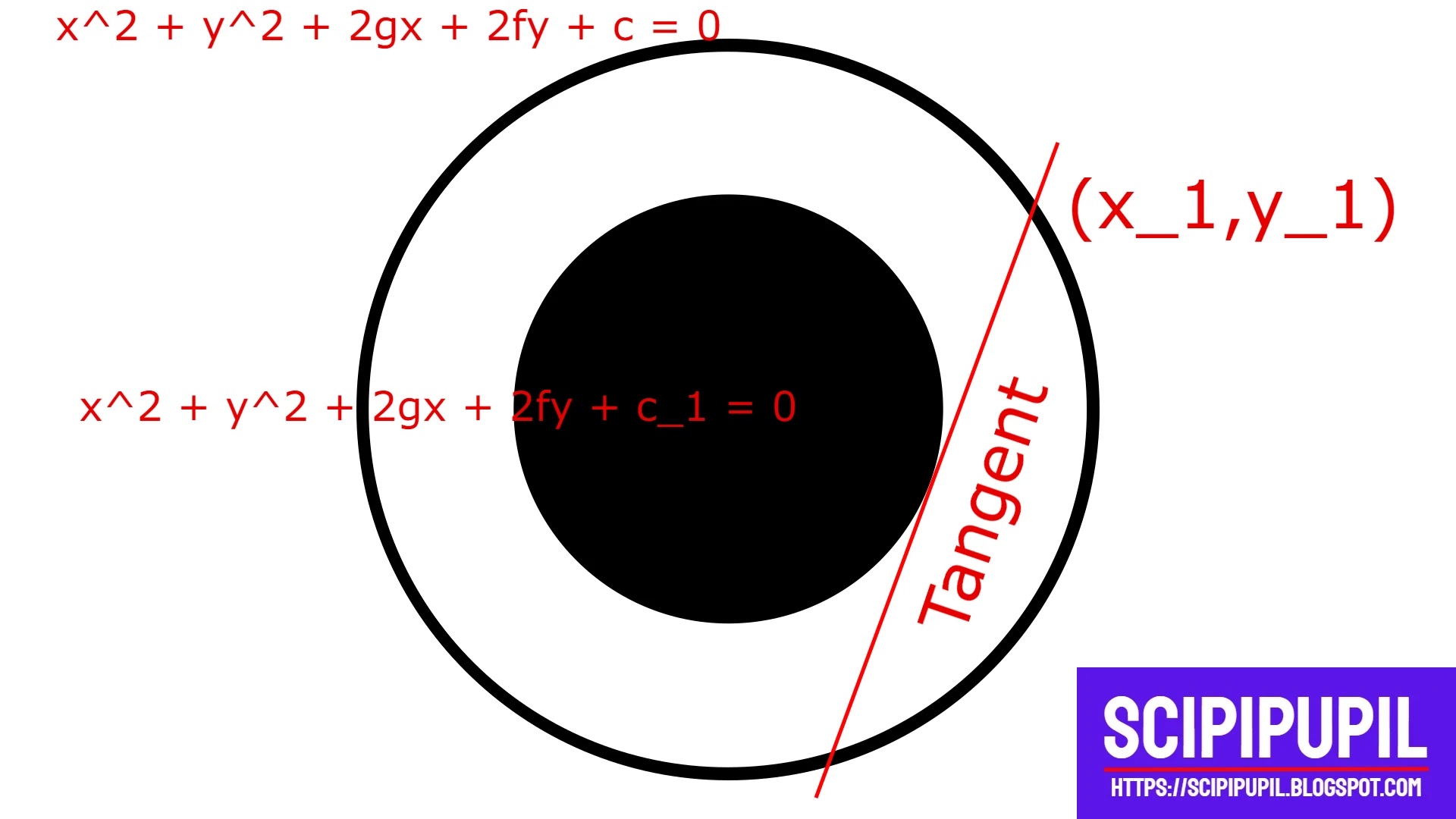
Both the circles have the same centres so they are concentric. Also, a tangent is drawn from the outer circle to the inner circle.
Let a tangent be drawn to the circle $x^2 + y^2 + 2gx + 2fy + c_1=0$ from
a point $(x_1,y_1)$ on circle $x^2 +y^2 + 2gx + 2fy + c = 0$.
Equation of point $(x_1,y_1)$ in circle $x^2 +y^2 + 2gx + 2fy + c = 0$ is $x_1^2 + y_1^2 + 2gx_1 + 2fy_1 + c =
0$
$\implies - c = x_1^2 + y_1^2 + 2gx_1 +2fy_1$
Now,
Length of tangent from point $(x_1,y_1)$ on circle $x^2 + y^2 + 2gx + 2fy + c_1=0$ is given by
$\sqrt{x_1^2 + y_1^2 + 2gx_1 + 2fy_1 + c_1}$
$\implies {-c + c_1}$
$\implies {c_1 -c }$
Hence, proved.
About the Textbook:
Name: Basic Mathematics Grade XI
Author(s): D.R. Bajracharya | R.M. Shresththa | M.B. Singh | Y.R.
Sthapit | B.C. Bajracharya
Publisher: Sukunda Pustak Bhawan (Bhotahity, Kathmandu)
Telephone: 5320379, 5353537
Price: 695 /- (2078 BS)
Buy this book: Basic Mathematics : Grade XI – Sukunda Publication


2 Comments
This comment has been removed by the author.
ReplyDelete2-8 ni upload garnuparyo daii
ReplyDeleteYou can let us know your questions in the comments section as well.