Geometry is the easiest portion of Mathematics in Class 10, if you exclude the out theorem which comes for 5 marks. Other questions are very easy to tackle and aren't much tricky.

Geometry is asked in all Groups i.e. Group A, Group B, Group C, and Group D.

In Group A, it is asked for 1 mark (1 question).

In Group B, it is asked for 4 marks (2 questions).

In Group C, it is asked for 12 marks (3 questions).

In Group D, it is asked for 5 marks (1 question).

Let us move to the solutions of Area of Triangles and Quadrilaterals from Geometry Chapter of Class 10.

Class 10 - Geometry - Area of Triangles and Quadrilaterals- Solved Exercises | vedanta Excel in Mathematics


General Section


Page 1 of 7

Page 2 of 7



Page 3 of 7

Page 4 of 7



Page 5 of 7



Page 6 of 7



Page 7 of 7



Creative Section

3 a) In the adjoining figure, ABCD and BCEF are parallelograms, AE//BC. Prove that: parm.ABCD = parm.BCEF.
In the adjoining figure, ABCD and BCEF are parallelograms, AE//BC. Prove that: parm.ABCD = parm.BCEF.


3 b): In the figure alongside, QR//PS. Prove that ∆PQR is equal to ∆QRS.


3 c) In the given figure, DX//AB. Prove that area of triangle.ABX = 1/2 area of parallelogram.ABCD.

In the given figure, DX//AB. Prove that area of triangle.ABX = 1/2 area of parm.ABCD.


3 d) In the given figure, ABCD is a parallelogram. X is any point within it. Prove that the sum of the areas of traingle.XCD and triangle.XAB is equal to half of the area of parallelogram.ABCD.

In the given figure, ABCD is a parallelogram. X is any point within it. Prove that the sum of the areas of traingle.XCD and triangle.XAB is equal to half of the area of parallelogram.ABCD.



3 e) In the adjoining figure, triangles AMB and ANB are standing on the same base AB and between the same parallel lines AB and MN. Prove that area of triangle.AOM = area of triangle.BON. 
In the adjoining figure, triangles AMB and ANB are standing on the same base AB and between the same parallel lines AB and MN. Prove that area of triangle.AOM = area of triangle.BON.


3 f) In the given figure, triangle.ABC and parallelogram.MBCN are on the same base BC and between the same parallels MN and BC. Prove that, area of triangle.ABC = area of rectangle.APCN.

In the given figure, triangle.ABC and parallelogram.MBCN are on the same base BC and between the same parallels MN and BC. Prove that, area of triangle.ABC = area of rectangle.APCN.


3 g) In the given parallelogram ABCD, X and Y are any points on CD and AD respectively. Prove that, area of triangle.AXB = area of triangle.BYC.

In the given parallelogram ABCD, X and Y are any points on CD and AD respectively. Prove that, area of triangle.AXB = area of triangle.BYC.


3 h) In the adjoining parallelogram ABCD, A is joined to any point E on BC. AE and DC produced meet at E. Prove that, area of triangle.BEF = area of triangle.CDE.

Correction: In the reason of statement number 7, instead of writing "Whole part axiom", you should be writing "Remaining part of whole".

In the adjoining parallelogram ABCD, A is joined to any point E on BC. AE and DC produced meet at E. Prove that, area of triangle.BEF = area of triangle.CDE.



3 i) In the given figure, rectangle PQRS and parallelogram AQRB on the same base QR and between the same parallels PB and QR. Prove that (i) triangle.PQA is congruent to triangle.SRB and (ii) Area of rectangle PQRS = Area of rectangle AQRB.

In the given figure, rectangle PQRS and parallelogram AQRB on the same base QR and between the same parallels PB and QR. Prove that (i) triangle.PQA is congruent to triangle.SRB and (ii) Area of rectangle PQRS = Area of rectangle AQRB.



3 j) In the adjoining parallelogram ABCD, PQ//AB and RS//BC. Prove that area of parallelogram.ROPA = area of parallelogram.OCSO.

In the adjoining parallelogram ABCD, PQ/AB and RS//BC. Prove that area of parm.ROPA = area of parm.OCSO.



3 k) In the given figure, ABCD is a parallelogram. If M and N are any points on CD and DA respectively, prove that triangle.AMB = triangle.CDN + triangle.ANB.

In the given figure, ABCD is a parallelogram. If M and N are any points on CD and DA respectively, prove that triangle.AMB = triangle.CDN + triangle.ANB.



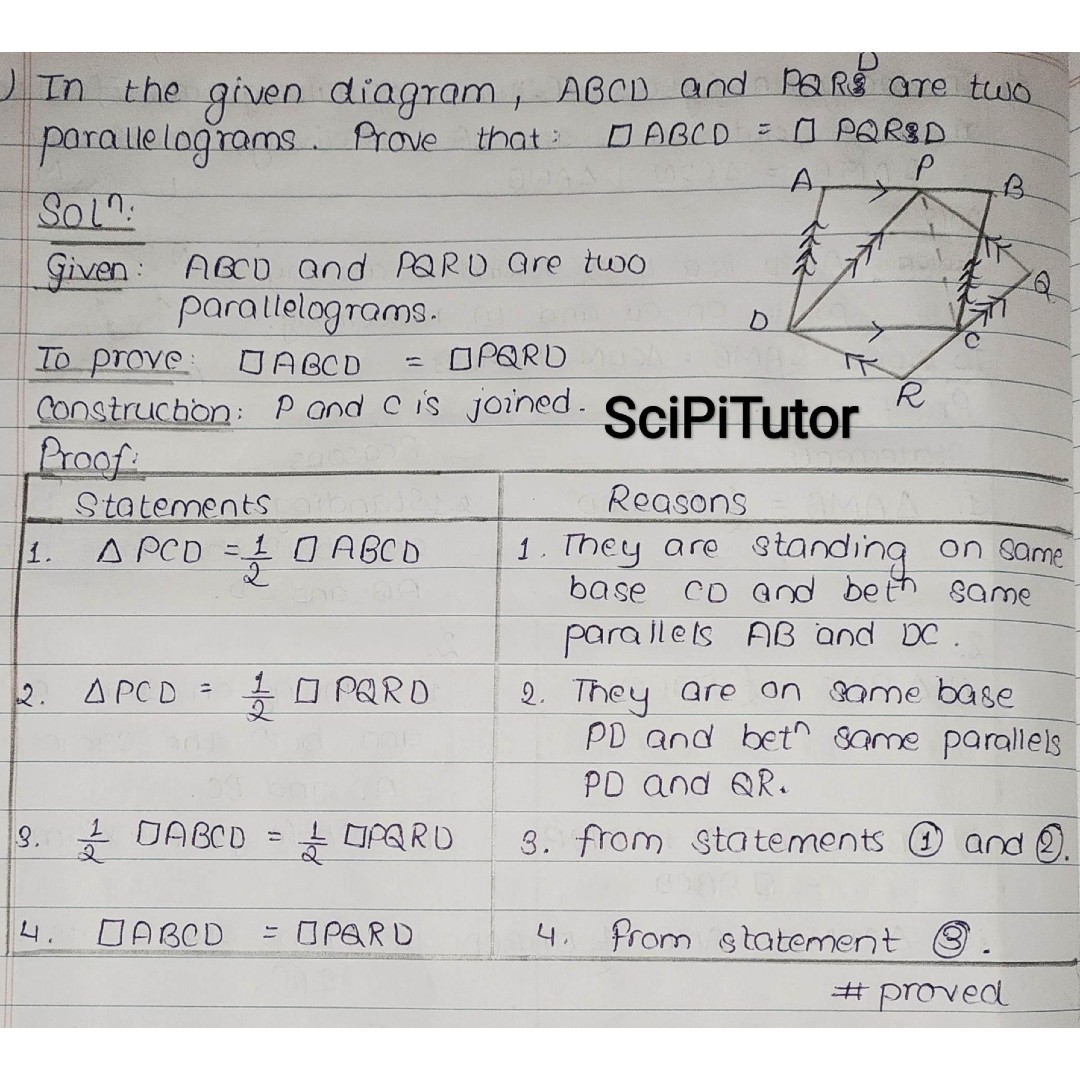
3 l) In the given diagram, ABCD and PQRD are two parallelograms. Prove that parm.ABCD = parm.PQRD.
In the given diagram, ABCD and PQRD are two parallelograms. Prove that parm.ABCD = parm.PQRD.


3 m) In the given figure, if AB//DC//EF, AD//BE and AF//DE, prove that parm.DEFH = parm.ABCD.
In the given figure, if AB//DC//EF, AD//BE and AF//DE, prove that parm.DEFH = parm.ABCD.




4 a) In the given triangle ABC, P is any point on the median AD. Prove that triangle APB = triangle APC.
In the given triangle ABC, P is any point on the median AD. Prove that triangle APB = triangle APC.


4 b) In the adjoining triangle ABC, P and Q are the mid-points of the sides AB and AC respectively and R be any point on BC. Prove that: area of triangle PQR = 1/4 area of triangle ABC.



4 c) In the figure, PQRS is a parallelogram. Q and S are joined to any point M on the diagonal PR. Prove that, area of triangle.PQM = area of triangle.PSM.

In the figure, PQRS is a parallelogram. Q and S are joined to any point M on the diagonal PR. Prove that, area of triangle.PQM = area of triangle.PSM.




4 d) In the given figure, DE//BC. Prove that: (i) triangle BOD = triangle COE and (ii) triangle BAE = triangle CAD.

In the given figure, DE//BC. Prove that: (i) triangle BOD = triangle COE and (ii) triangle BAE = triangle CAD.



4 e) In the given figure, P is the mid-point of AB and Q is any point on the side BC. CR meets AB at R and CR//PQ. Prove that, area of triangle BQR = 1/2 area of triangle ABC.

In the given figure, P is the mid-point of AB and Q is any point on the side BC. CR meets AB at R and CR//PQ. Prove that, area of triangle BQR = 1/2 area of triangle ABC.




4 f) The line drawn through the vertex C of the quadrilateral ABCD parallel to the diagonal DB meets AB produced at E. Prove that, area of quad. ABCD = area of triangle DAE.
The line drawn through the vertex C of the quadrilateral ABCD parallel to the diagonal DB meets AB produced at E. Prove that, area of quad. ABCD = area of triangle DAE.



4 g) In the given triangle ABC, two medians BE and CD are intersecting at O. Prove that, area of triangle BOC = area of quadrilateral ADOE.

In the given triangle ABC, two medians BE and CD are intersecting at O. Prove that, area of triangle BOC = area of quadrilateral ADOE.



4 h) In the adjoining figure, it is given that AD//BC and BC//CE. Prove that, area of triangle.ABC = area of triangle.BDE.
In the adjoining figure, it is given that AD//BC and BC//CE. Prove that, area of triangle.ABC = area of triangle.BDE.




4 i) In the given figure, BEST is a parallelogram. Diagonal BS is produced to point L. Prove that: triangle LST and triangle LSE are equal in area.




4 j) In the given figure, AD//BC. If the area of triangle ABE and triangle ACF are equal, then prove that EF // AC.




4 k) In the given figure, Ad//BE//GF and AB//DG//EF. If the area of parallelograms ABCD and CEFG are equal, then prove that DE // BG.




4 l) In the adjoining figure, PQRS and LQMN are two parallelograms of equal in area. Prove that LR // SN.




4 m) In the given triangle ABC, medians BN and Cm are intersected at O. Prove that: Area of triangle BOC = Area of quadrilateral AMON.




4 n) In the given figure, M is the mid-point of AE, then prove that area of triangle ABE is equal to the area of parallelogram ABCD.

4.

a)

b) Answer has not been updated yet! 

c)

d)

e)

f)

g)


h)


About vedanta EXCEL in MATHEMATICS Book 10

Author: Hukum Pd. Dahal
Editor: Tara Bahadur Magar

Vanasthali, Kathmandu, Nepal
+977-10-4382404, 01-4362082
vedantapublication@gmail.com

About this page:


Class 10 - Geometry - Area of Triangles and Quadrilaterals- Solved Exercises | vedanta Excel in Mathematics is a collection of the solutions related to theorem proofs of figures related to the area of triangles and quadrilaterals of geometry chapter for Nepal's Secondary Education Examination (SEE) appearing students.

#Class10